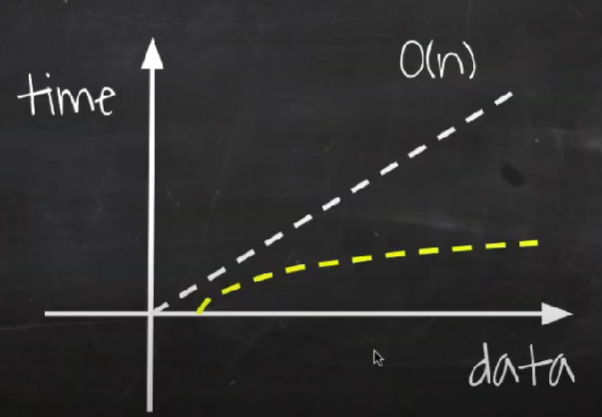
빅오 표기법(Big O Notation)이란?
- 알고리즘의 성능을 수학적으로 표기해주는 표기법
- 최악의 경우의 시간 복잡도를 의미
- 빅오 표기법을 통해 성능을 개선하거나 적절한 알고리즘을 선택할 수 있다.
복잡도
- 시간 복잡도(Time Complexity)
CPU가 처리하는 데 걸리는 시간 → 수치가 작을수록 효율적인 알고리즘 - 공간 복잡도(Space Complexity)
처리하는 데 사용되는 메모리 크기 (RAM 사용량) → 메모리 사용량이 적을수록 효율적인 알고리즘
최악의 경우의 시간 복잡도
- 알고리즘이 입력 크기에 따라 가장 오래 걸리는 경우
- 최악의 경우의 시간 복잡도를 분석함으로써 알고리즘을 설계할 때 최악의 성능을 예측하고, 최악의 경우에도 어느 정도의 실행 속도를 보장함을 확인한다.
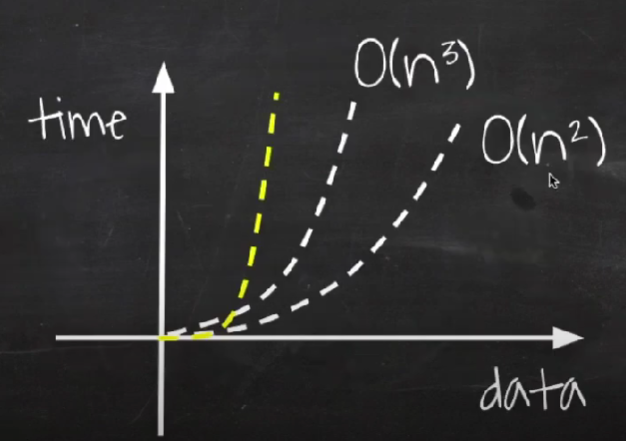
빅오 복잡성 차트(Big-O Complexity Chart)

| 표기법 | 이름 | 시간 복잡도 | 설명 | 예시 |
| O(1) | 상수 | 상수 시간 | 입력 크기와 상관 없이 일정한 실행 시간을 가진다. | 배열에서 원소 하나 찾기 |
| O(n) | 선형 | 선형 시간 | 입력 크기와 비례하는 실행 시간을 가진다. | 선형 탐색 알고리즘 |
| O(n^2) | 이차 | 이차 시간 | 입력 크기의 제곱에 비례하는 실행 시간을 가진다. | 선택 정렬, 버블 정렬, 퀵 정렬 알고리즘 |
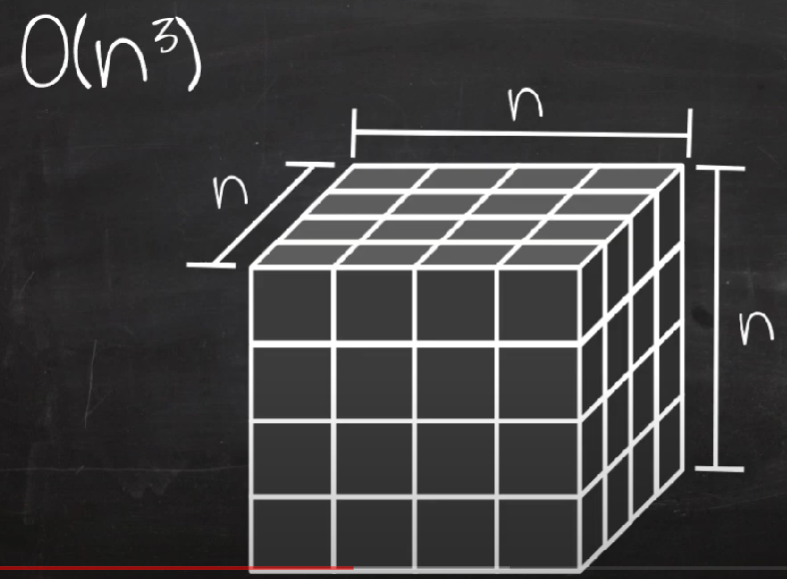
| O(n^3) | 삼차 | 삼차 시간 | 입력 크기의 세제곱에 비례하는 실행 시간을 가진다. | 루프 3번 돌리기 |
| O(2^n) | 지수 | 지수 시간 | 입력 크기의 지수에 비례하는 실행 시간을 가진다. | 부분집합 |
| O(log n) | 로그 | 로그 시간 | 입력 크기가 증가함에 따라 실행 시간이 로그 함수의 형태로 증가한다. | 이진 탐색 알고리즘 |
표기법 예시
O(1): 상수 시간 알고리즘
public static boolean F(int[] n) {
return (n[0] == 0)? true:false;
}데이터가 증가함에 따라 성능에 변함이 없다.

O(n): 선형 시간 알고리즘
//n의 크기에 비례해서 처리 시간이 소요된다.
public static void F(int[] n) {
for(int i=0; i < n.length; i++) {
System.out.println(i);
}
}입력 데이터의 크기에 비례해서 처리 시간이 걸리는 알고리즘

O(n^2): 이차 시간 알고리즘
public static void F(int[] n){
for(int i=0; i < n.length; i++){
for(int j=0; j < n.length; j++){
System.out.println(i + j);
}
}
}
O(n^3): 삼차 시간 알고리즘
public static void F(int[] n){
for(int i=0; i < n.length; i++){
for(int j=0; j < n.length; j++){
for(int k=0; k < n.length; k++){
System.out.println(i + j + k);
}
}
}
}

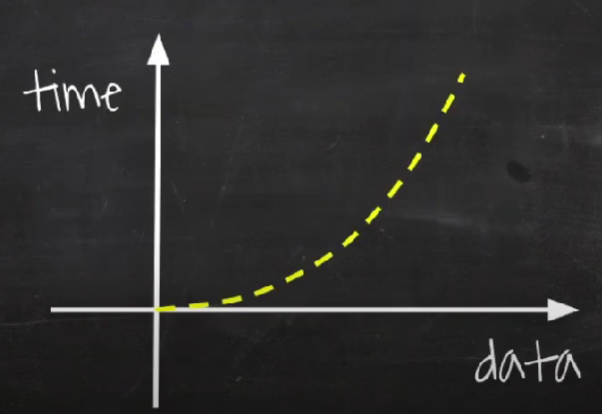
O(2^n): 지수 시간 알고리즘
피보나치 수열
1, 1, 2, 3, 5, 8, ...
public static int fibonacci(int n) {
if (n <= 1) {
return n;
}
return fibonacci(n - 1) + fibonacci(n - 2);
}
O(log n): 로그 시간 알고리즘
이진 검색 알고리즘
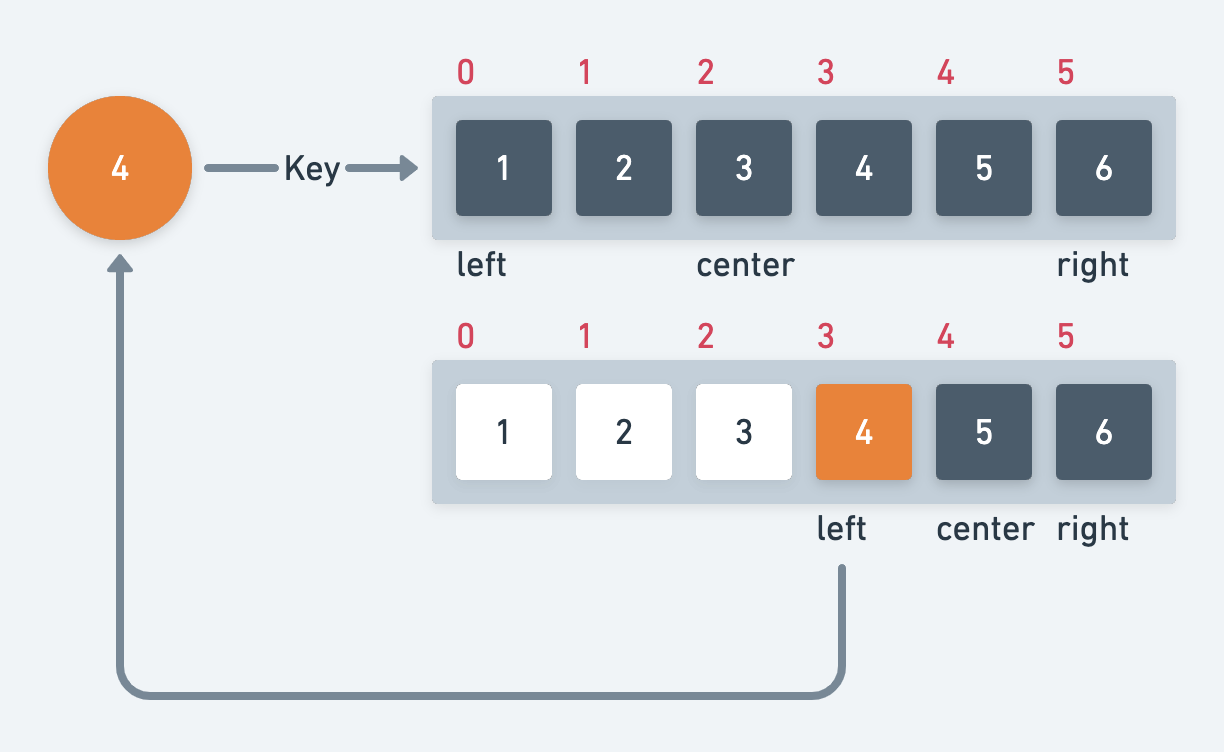
- 이미 정렬되어 있는 배열에서 범위를 좁혀가며 값을 찾는 탐색법
- 선형 탐색보다 속도가 빠르다.
- left = 탐색 시작 위치
- center = 탐색 중앙 위치 ((n-1) / 2)
- right = 탐색 끝 위치 (n-1)
- 중앙 요소가 찾는 key보다 작을 때 (center + 1) ~ right까지 탐색 범위를 좁힌다.
- 중앙 요소가 찾는 key보다 클 때 left ~ (center - 1)까지 탐색 범위를 좁힌다.
public static int binarySearch(int[] arr, int n, int key) {
Arrays.sort(arr); //오름차순으로 정렬하고 시작
System.out.println("----------오름차순 정렬 후---------------");
System.out.println(Arrays.toString(arr));
System.out.println("--------------------------------------");
int left = 0;
int right = n-1; //n = 배열의 크기
int center = 0; //중앙 위치의 인덱스 연산
//반복문 돌면서 배열의 중앙 위치에 저장된 값과 key값을 비교
int cnt = 0;
while(left <= right) {
cnt++;
center = (left + right)/2; //중앙값
if(key == arr[center]) {
System.out.println(cnt + "번 만에 찾았습니다.");
return center;
}else if(key > arr[center]) {
left = center + 1;
}else {
right = center - 1;
}
}
return -1;
}